#Day29 #100DaysOfCode
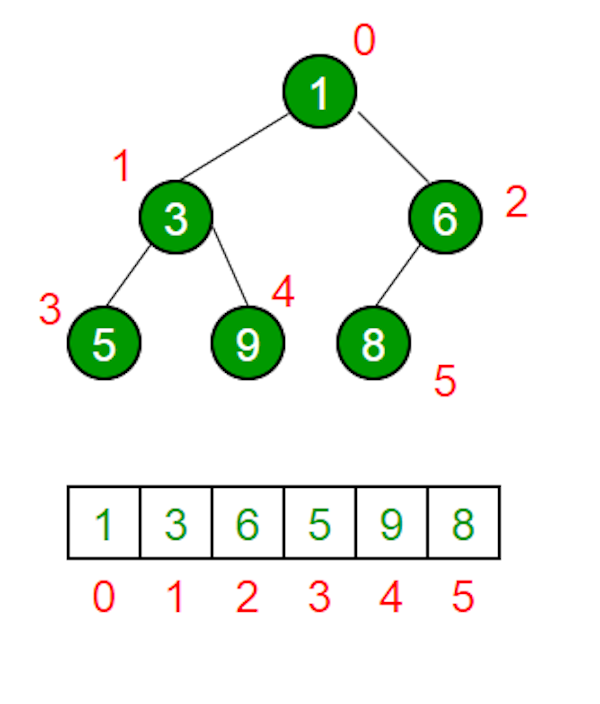
Binary Heap is a data structure that requires knowledge of both trees and arrays. In fact, it is a complete binary tree, but is represented in a 1d array. See my previous blogs for properties of a complete binary tree.
Some basic operations with a binary heap are heapify, insert a node, delete a node, getmin, extract min, parent, left. right. All involves with heapify, since when an operation violates the heap property (either larger or smaller than parent), heapify is called.
overall and worst time complexity for insert and delele a node to/from a tree is O(logn) since the worst case happens when moving a node from the leaf to the root, which is passed through the tree height logn, where n is the number of nodes.
Best case for both insert and delete is O(1). For example, insert a node that doesn't violate the heap property, or delete the last leaf.
Binary Heap is a data structure that requires knowledge of both trees and arrays. In fact, it is a complete binary tree, but is represented in a 1d array. See my previous blogs for properties of a complete binary tree.
Some basic operations with a binary heap are heapify, insert a node, delete a node, getmin, extract min, parent, left. right. All involves with heapify, since when an operation violates the heap property (either larger or smaller than parent), heapify is called.
overall and worst time complexity for insert and delele a node to/from a tree is O(logn) since the worst case happens when moving a node from the leaf to the root, which is passed through the tree height logn, where n is the number of nodes.
Best case for both insert and delete is O(1). For example, insert a node that doesn't violate the heap property, or delete the last leaf.